Note If the images do not appear change the file-extention to dot, and you can download the raw file and use xdot to recreate the images.

Language Instances as Graphs

On Tuesday, 7th June 2022 I was fortunate enough to attend the Huawei Coffee House talk on port graphs by Maribel Fernández. An interesting comment made by Maribel, and some audience members, was that we should not think about derivations (i.e. used in the type checking process or to describe evaluation) as tree but rather we view them as graphs. Such a mindset easily supports visualisation of properties such as confluence: evaluation of a term will, regardless of strategy, will result in the same value.

We already use such a view on our language’s terms when using Abstract Syntax Trees in which nodes are terms and edges link terms with their sub-terms. A more interesting variant is that of an abstract syntax graph in which are terms are nodes and edges are bound variables. At the end of the day, and regardless of if you use ASTs or ASGs, both capture language structure as a graph.

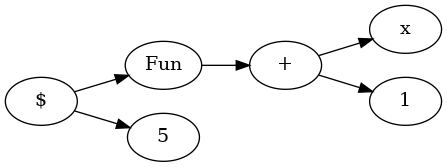
When type-checking our terms we can instead think not about building derivation trees but building a derivation graph such that if we encounter a type-error we cannot build the graph. Now these graphs will be directed. Take for example, the simple Lambda term, which we express in a simple function application (the STLC) using S-expression inspired syntax:

($ (\x:Nat.(+ x 1))
   5)

Which we can visualise as:

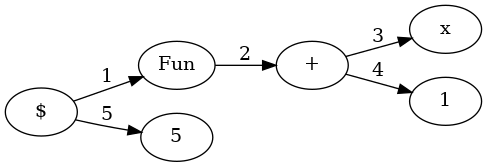
Type-Checking is all about Communicating Processes

Many years ago, Conor Mc Bride gave a Shameless PLUG in which he made the realisation that type-checking is a communication game in which types and terms are servers that communicate their information (types) to each other. Taking a more simplified approach we can use this to describe how type-checking of terms work if we assume that our languages terms are in fact communicating processes.

For statically typed languages, this equates to a multicast through the network with each server being asked to check it’s own type according to the language’s rules. In terms of graph theory this results in a depth-first search of the graph checking if each vertex, and its child vertices, are well-typed.

Bi-Directional Typing is the Truth.

Now we all know that how we teach type-checking is wrong ¹_, and bi-directional type-theory codifies how we actually do it. Essentially, the standard type signature for a type-checker is:

tyCheck : Context -> Term -> Either Error Ty

this is wrong! We are not checking if the term has the correct type, rather we are asking the term what its type is. This is otherwise known as type-synthesis. Bi-directional type-theory formalises when we need to check a term’s type, given some information we already know, and when we need to ask (synthesise) the type. This results in two co-recursive functions:

synth : Context -> Term -> Either Error Ty

and

check : Context -> Ty -> Term -> Either Error ()

Well in Conor’s talk he specifically mentions that the checking and asking of information between a term and it’s type is the communication we need for type-checking.

New Terms

Now before we look at how this relates to type-checking and graph traversal, we need to realise that with bi-directional type-systems we need two introduce new terms that support switching from checking to synthesising and vice-versa.

Thus, the set of terms for the STLC (with addition of natural numbers) will actually be:

t : TYPE ::= Nat | (t -> t)
e : t    ::= n | x | (fun x e) | ($ e e) | (+ e e)
           | (Check t e) -- currently synthesising start checking
           | (Synth   e) -- currently checking start synthesing

This will lead to a new visual representation of our graph. Which we present below with annotations on vertices to see if a term is checkable (C) synthesisable (S), or a type (TYPE).

The textual representation would be:

($ (Check (Nat -> Nat)
          \x:Nat.(+ (Synth x)
                     1))
   5)

Again edges present the flow of information! But this isn’t the whole story.

Communication is a two way street.

Specifically, if we are employing a bi-directional type-system and treating it as a communication protocol we need to model the synchronicity of the communication. Commands and responses! Thus we have to updated our new graph with edges to capture the responses. We will also label them so that we can see the order, and present a starting/end server.

If we enumerate the steps as an informal protocol narration we get something like this:

(0)  Alpha/Omega -> $           | Asks: Are you well-typed?
(1)  $           -> \ni         | Asks: Are you a function?
(2)  \ni         -> Store       | Ponders: What is my type?
(3)  Store       -> \ni         | Responds: I am (Nat -> Nat)!
(4)  \ni         -> Fun         | Checks: Are you (Nat -> Nat)?
(5)  Fun         -> +           | Checks: Are you a Nat?
(6)  +           -> Store       | Ponders: What is my type?
(7)  Store       -> +           | Responds: I am (Nat)!
(8)  +           -> Synth       | Checks: Are you a Nat?
(9)  Synth       -> x           | Asks: Are you really Nat?
(10) x           -> Synth       | Responds: Of Course!
(11) Synth       -> +           | Responds: I am (Nat)!
(12) +           -> 1           | Checks: Are you a Nat?
(13) 1           -> +           | Responds: I am (Nat)!
(14) +           -> Fun         | Responds: I am (Nat)!
(15) Fun         -> \ni         | Responds: I am (Nat -> Nat)!
(16) \ni         -> $           | Responds: I am (Nat -> Nat)!
(17) $           -> 5           | Checks: Are you a Nat?
(18) 5           -> $           | Responds: I am (Nat)!
(19) $           -> Alpha/Omega | Responds: I am Spartacus!

Why should we care?

Well one way to think about type-checking is not to see if our terms are well-typed, but as:

Can we build a graph with the communication structure required for typing, and follow an ordered communication trail from the root vertex back to itself!

Formally a trail is a walk of a graph that visits uses each edge once.

This is exciting, as it is another way to think about type-checking and linking it to some well-studied mathematical techniques (graphs), and to give it a modern twist (network communication).

Coda

I do not know if I will visit this idea further as, unfortunately, I have other stuff to do. Part of me does hope so, as it is an interesting way to visualise, and reason about, type-checking.

Funnily enough a project student of mine from a few years ago did visualise type-checking as a graph. I as a little annoyed as I wanted derivation trees rather than a graph traversal. Oh how I was wrong…

If you are interested in the Type-Checking as a Communicating Processes then check out TypOS by the MSP gang².

If you are interested in visualising, and reasoning about, languages as graph please check out the work of Dan Ghica.